cnn
约 1862 字大约 6 分钟
2025-12-27
CNN(Convolutional Neural Network)是一种 专门处理图像 的神经网络。
相比 MLP(全连接层),CNN 的参数少很多,提取图像局部特征能力更强。
[TOC]
卷积层(Convolutional Layer)
这是 CNN 的核心。它使用卷积核(Kernel)在图像上滑动,提取局部特征。
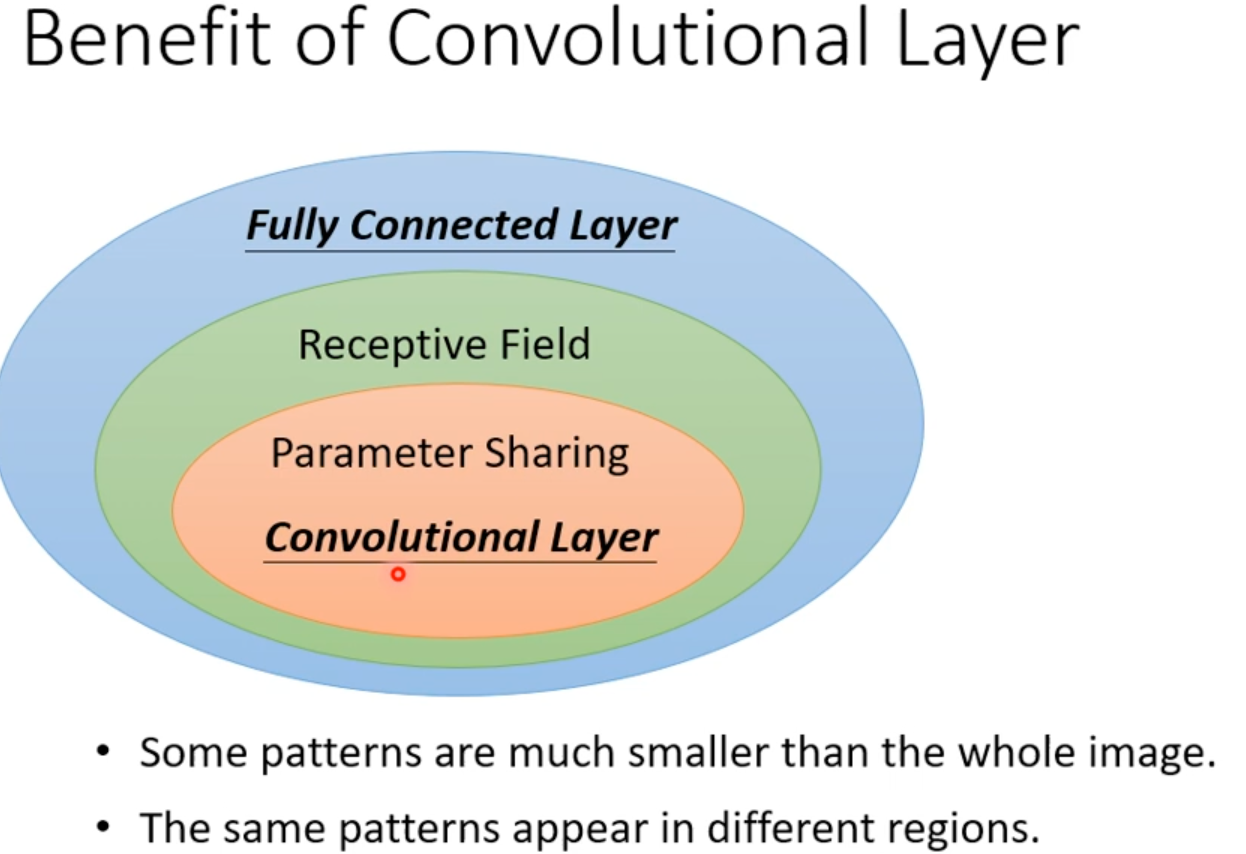
1. 感受野(Receptive field)和卷积核大小(Kernel Size)
感受野:这是输出特征图(Feature Map)上的一个像素点,在原始输入图像(Input Image)上所能“看到”或者是“映射”到的区域大小。
卷积核大小:这是卷积层的一个超参数(Hyperparameter)。它定义了在进行卷积操作时,滑动窗口的长和宽。
这是理解两者区别最关键的地方:小的 Kernel Size 可以通过堆叠(Stacking)产生大的 Receptive Field。
经典案例(VGG 网络): VGG 网络证明了,使用两个堆叠的 3×3 卷积层,其感受野等于一个 5×5 卷积层;使用三个堆叠的 3×3 卷积层,其感受野等于一个 7×7 卷积层。
2. 参数共享(Parameter Sharing)
也叫权重共享(Weight Sharing),是深度学习(尤其是 CNN 和 RNN)中减少模型参数数量、提高训练效率的核心机制。
同一个卷积核(kernel)会在整张图片的不同位置重复使用,权重不变。因为在图像中,同一个特征在任何位置都是同一个特征!
3. 特征图(Feature Map)
特征图 = 卷积层输出的图,是图片在卷积核作用下提取到的某一种特征的响应图。
激活层(Activation Layer)
通常跟在卷积层后面。最常用的是 ReLU (Rectified Linear Unit)。
引入非线性。如果没有它,多少层卷积叠加最后都等价于一层线性变换。ReLU 就像一个开关,把负值(无用的信号)砍掉,只保留正值(有用的特征激活),让网络能拟合复杂的形状。
池化层(Pooling Layer)
把图片变小,减少参数量和计算量。让模型对物体的位置微小移动不那么敏感(比如猫稍微向左移一点,Max Pooling 取最大值可能还是一样,特征依然能被保留)。
- 降低采样率(降采样)
- 提升鲁棒性
- 抑制噪声
常见有最大池化和平均池化。
ResNet架构
1. 由来
超深的网络结构(突破1000层)
如果简单堆叠(不是层数越深效果越好):
a. 梯度消失:假设每一层的误差梯度是小于1的数,反向传播过程中每向前传播一层,都要乘以一个小于1的误差梯度。当网络越来越深时,所乘的小于1的系数就越多,梯度就越趋近于0。
b. 梯度爆炸:假设每一层的误差梯度是大于1的数,反向传播过程中每向前传播一层,都要乘以一个大于1的误差梯度。当网络越来越深时,梯度越来越大。
c. 解决梯度消失和梯度爆炸的方法:数据进行标准化处理,权重初始化,BN
d. 退化问题:层数深没有层数浅的网络效果好
2. 残差结构
ResNet不让网络去学:H(x) (最终想要的输出)
而是让它学:F(x) = H(x) - x
最后:输出 = x + F(x)
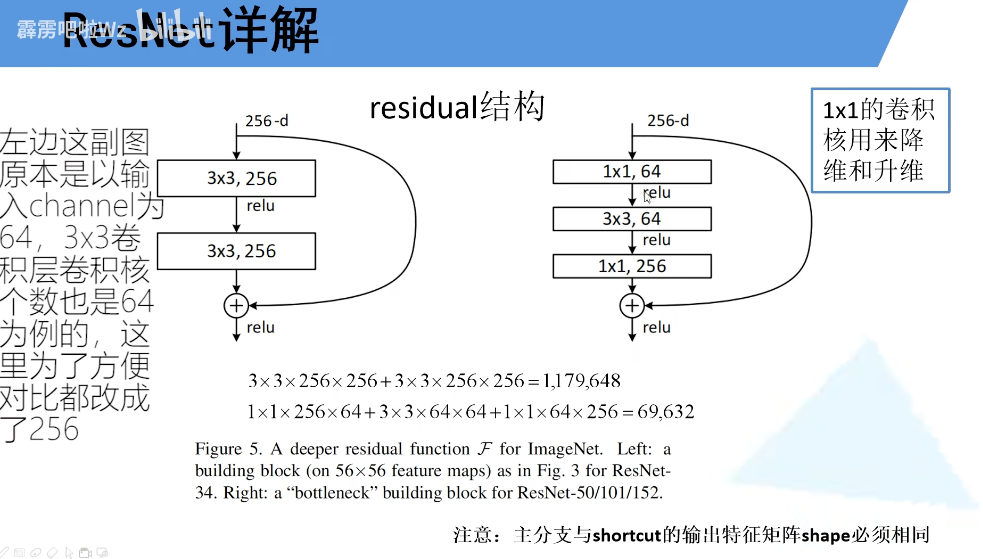
左边针对与网络层数较少的的网络所使用的的残差结构(34),右边主要针对与网络层数较多的网络所使用的结构(50/101/152)。主分支与侧分支的输出矩阵特征shape必须相同(高宽通道数相同)。右边在输入和输出都加上了1X1的卷积层,降维再升维(256→64→256),保证shape相同的情况下减少参数。使用的残差结构越多,减少的参数就越多。
3.实线残差结构和虚线残差结构
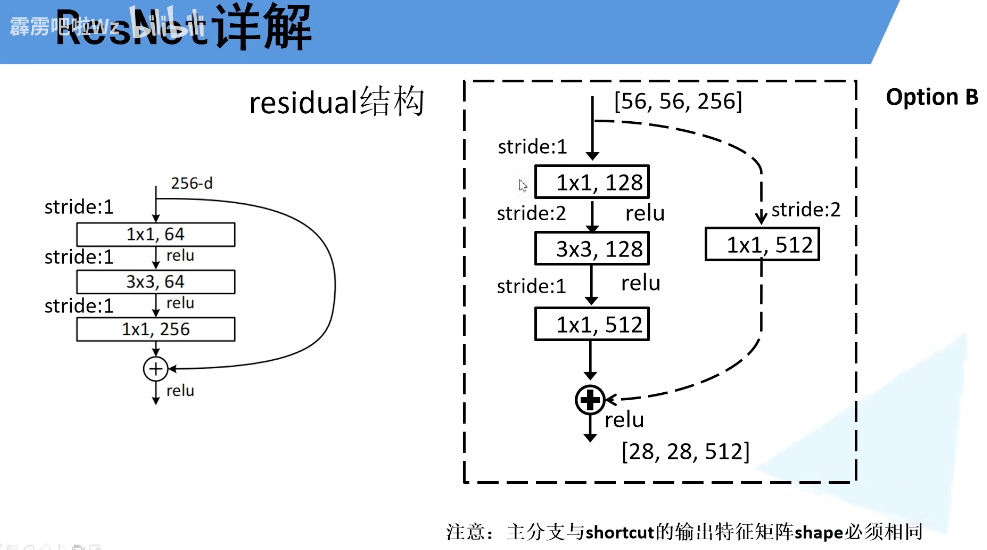
实线残差结构:输入输出shape相同,可以直接相加。
虚线残差结构:输入输出矩阵shape不同,输入:【56,56,64】,输出:【28,28,128】,只有将虚线残差结构的输出输入到实线残差结构,才能保证输入输出矩阵的shape相同。
4.最后的整个CNN
ResNet = 卷积 stem + 多个 stage 每个 stage = 多个残差块堆叠 stage 之间:降分辨率、升通道
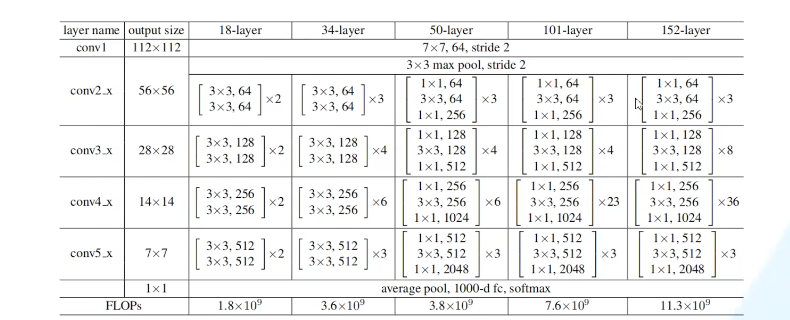
- 对于浅层网络(18 34):
conv3x,conv4x,conv5x的第一层均采用虚线残差结构
通过最大池化下采样得到的输出【56,56,64】,刚好是实线残差结构所需要的输入shape,此时conv2x第一层不需要使用虚线残差结构。
- 对于深层网络(50/101/152):
通过最大池化下采样得到的输出【56,56,64】,而所需的shape为【56,56,256】,此时conv2x第一层需要使用虚线残差结构,但仅改变特征矩阵的深度,不改变高宽。
Batch Normaliztion
Batch Normalization (批归一化) 是一种在神经网络每一层输入之前(或激活函数之前)对数据进行标准化的技术。它强制将一个 Mini-Batch 中数据的分布调整为均值为 0,方差为 1 的标准正态分布,并通过可学习的参数还原数据的表达能力。
为什么需要 BN?
在深度神经网络训练过程中,前层参数的变化会导致后层输入数据的分布发生变化。
- 后果:后层网络需要不断适应新的输入分布,导致训练变慢;容易陷入饱和区(如 Sigmoid 梯度消失);对初始化参数非常敏感。
- BN 的作用:固定了每层输入的均值和方差,让网络“如履平地”,不再需要为了适应分布变化而浪费训练时间。
步骤
假设一个 Mini-Batch 的大小为 m,输入数据集合为 B={x1,x2,…,xm}。
1: 计算均值
计算当前 Batch 中所有样本的平均值:
μB=m1i=1∑mxi
2: 计算方差
计算当前 Batch 的方差:
σB2=m1i=1∑m(xi−μB)2
3: 归一化 (Normalize)
将数据标准化为均值 0、方差 1 的分布(ϵ 是防止分母为 0 的微小常数,如 1e−5):
x^i=σB2+ϵxi−μB
4: 缩放和平移 (Scale and Shift)
引入两个可学习参数 γ (缩放) 和 β (平移),让网络有能力恢复原始分布:
$ y_i = \gamma \hat{x}_i + \beta $
为什么要步骤 4?
如果强制将数据限制在 N(0,1),对于 Sigmoid/Tanh 等激活函数,数据会集中在线性区域,导致非线性表达能力下降。γ 和 β 允许网络自动学习是否需要保留归一化,或者恢复到某种特定分布。
维度理解(对于CNN)
在卷积神经网络(CNN)中,BN 是Channel-wise(按通道)进行的。
假设输入特征图张量为 (N,C,H,W):
- N: Batch Size
- C: Channel (通道数)
- H,W: Height, Width
BN 会把 同一个 Channel 下的所有样本、所有像素 放在一起计算均值和方差。
- 统计范围:(N,H,W) 作为一个整体。
- 参数数量:每个 Channel 对应一对 γ 和 β,所以参数总量是 2×C。
